Quantum computing is an incredibly promising field with the potential to revolutionize the way we process information and solve complex problems. However, one of the biggest challenges facing the development of quantum computers is the issue of error correction. In a recent publication in Science Advances, Hayato Goto from the RIKEN Center for Quantum Computing in Japan introduced a novel approach to quantum error correction using what he calls “many-hypercube codes.” This new method presents an elegant geometry that could significantly improve error correction efficiency and contribute to the realization of fault-tolerant quantum computing.
Traditionally, quantum error correction methods have focused on encoding a single logical qubit onto multiple entangled physical qubits and then using a decoder to retrieve the logical qubit. However, scalability has been a major issue with this approach, as the number of physical qubits required increases drastically, leading to resource overheads. To address this challenge, high-rate quantum codes like quantum low-density parity-check codes have been explored. While these codes offer higher efficiency, they often require sequential setup of logical gates, diminishing their time efficiency.
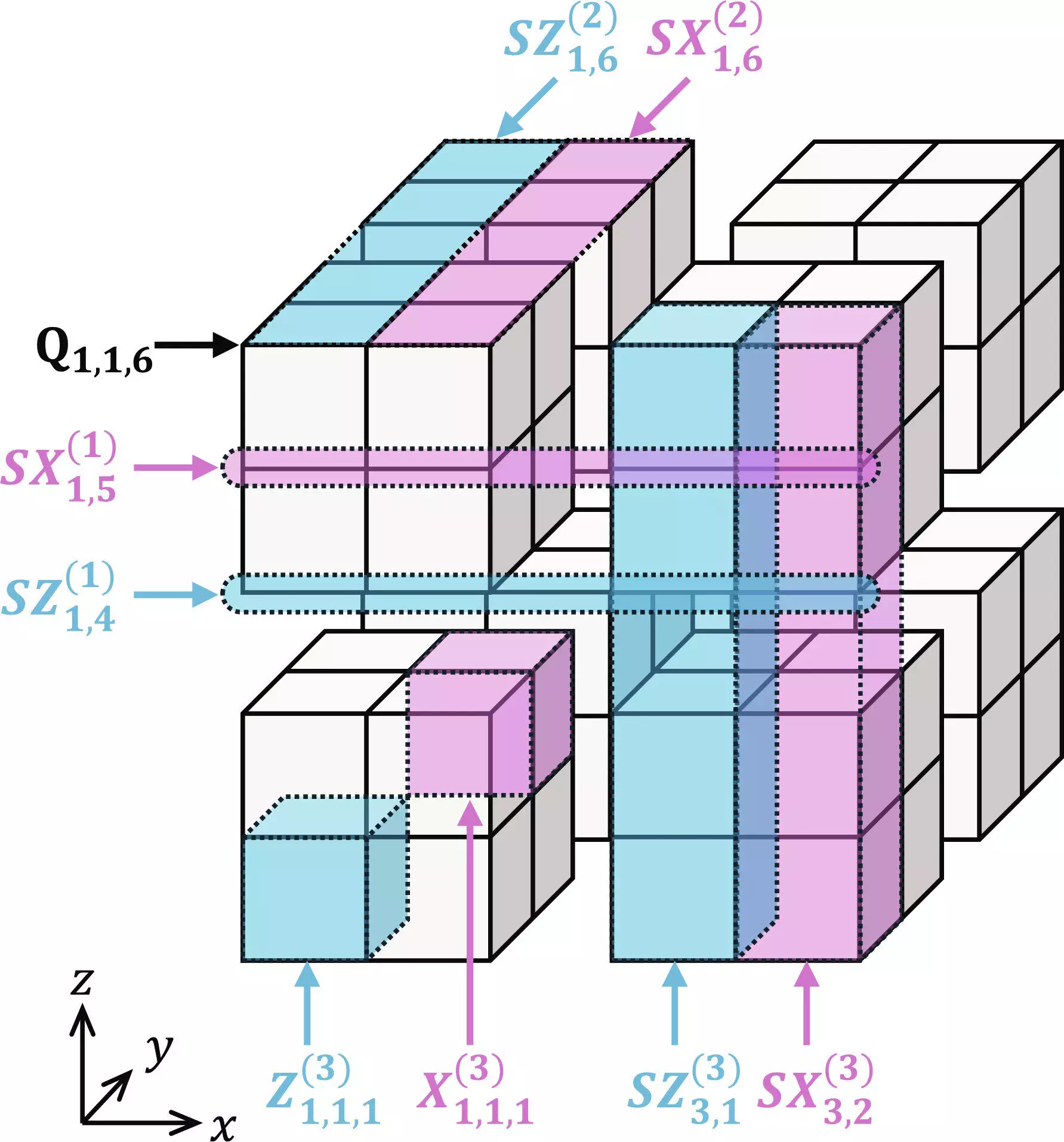
Hayato Goto’s proposed approach of using many-hypercube codes introduces a new perspective on quantum error correction. By visualizing logical qubits as forming hypercube structures, Goto has developed a method with a unique mathematical and geometric foundation. The codes exhibit a high encoding rate of up to 30%, which Goto claims to be the world’s highest among fault-tolerant quantum computing codes. This innovation allows for logical gates to operate in parallel, akin to parallel processing in classical computers, leading to what Goto describes as “high-performance fault-tolerant computing.”
A key aspect of Goto’s approach is the development of a dedicated decoder that can efficiently interpret the results from physical qubits. This decoder leverages level-by-level minimum distance decoding, enabling high performance in error correction. Unlike traditional methods, Goto’s approach allows for logical gates to function in parallel, maximizing system efficiency. The innovation in decoder design is crucial for enhancing the performance of many-hypercube codes and is a significant contribution to the field of quantum error correction.
The introduction of many-hypercube codes represents a significant advancement in the development of fault-tolerant quantum computing. By achieving high encoding rates and performance comparable to conventional low-rate codes, Goto’s approach paves the way for more efficient and reliable quantum computations. The elegant geometry and innovative decoder design of many-hypercube codes hold great promise for the future of quantum error correction and the realization of fault-tolerant quantum computers.
The exploration of new approaches to quantum error correction, such as the use of many-hypercube codes, is essential for overcoming the scalability challenges of current methods. The work by Hayato Goto demonstrates the potential for more efficient and high-performance fault-tolerant quantum computing systems. As the field of quantum computing continues to advance, innovative solutions like many-hypercube codes will play a crucial role in unlocking the full potential of quantum technologies.

Leave a Reply