The realm of quantum computing has witnessed remarkable strides, propelled by collaborative efforts from leading researchers who seek to address fundamental challenges in quantum mechanics. A notable endeavor is the research spearheaded by teams from Freie Universität Berlin, University of Maryland, Google AI, and NIST, among others, aiming to robustly estimate parameters related to bosonic excitations within superconducting quantum simulators. Their novel approaches, as discussed in their recent article on arXiv, promise to push the envelope towards sophisticated quantum simulations, extending far beyond classical computation capabilities.
The journey began when Jens Eisert, a pivotal figure in the project, received an urgent call from colleagues in the Google AI team during an event in Brazil. They sought assistance in calibrating their Sycamore quantum processor, encountering significant obstacles within Hamiltonian learning parameters. Initially, Eisert believed the solution would be straightforward; however, upon deeper contemplation, he recognized the complexity of the challenges that lay ahead.
As Eisert collaborated with talented Ph.D. candidates, namely Ingo Roth and Dominik Hangleiter, they initially believed they could apply superresolution techniques to tackle the problems they faced. However, it was not until several years later that the team’s efforts matured into a method robust enough for large-scale experiments. The persistence of Pedram Roushan, the lead experimentalist on the Google AI team, coupled with strong data outputs, proved instrumental in their eventual success.
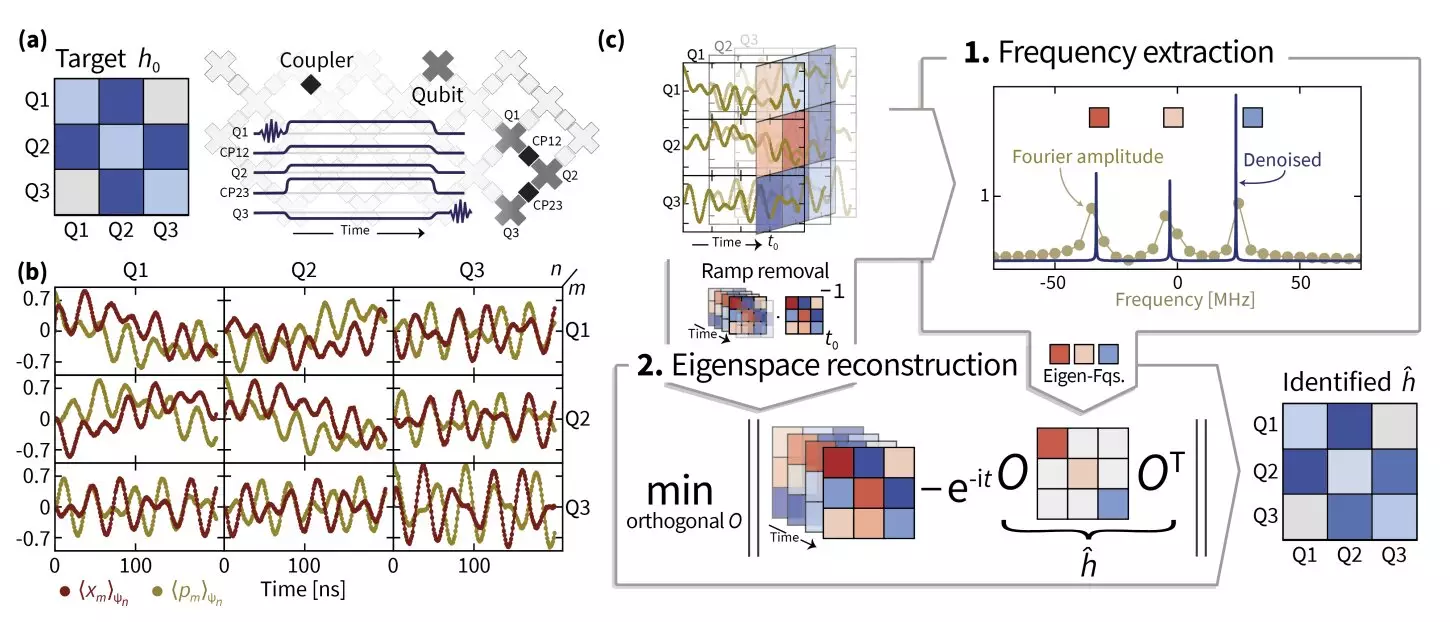
In their research, the team adopted a multifaceted approach to decipher the Hamiltonian dynamics of their superconducting quantum simulator. They began with superresolution techniques, aiming to refine the precision of the eigenvalue estimates to identify the Hamiltonian frequencies accurately. The subsequent step incorporated manifold optimization — an advanced method that aids in solving intricate problems characterized by their inherent geometric constraints.
Eisert emphasized the importance of understanding the processes involved in Hamiltonian dynamics and the significance of achieving accurate eigenvalue estimates for meaningful eigenspace recovery. The development of their method, duly named TensorEsprit, emerged as a groundbreaking approach to facilitate the recovery of Hamiltonian parameters for systems comprising multiple coupled superconducting qubits.
The Significance of Robustness in Quantum Simulations
One of the key revelations in Eisert’s work pertains to the challenges that accompany Hamiltonian learning in practical settings. The complexities of real-world data can introduce substantial noise, complicating the fitting processes of Hamiltonian models. The researchers discovered that improvements in signal processing methodologies, particularly those encapsulated in TensorEsprit, allow for greater resiliency in identifying Hamiltonian parameters even as system sizes increase.
Initial validations of their techniques indicated scalability, suggesting that the methods could be applied effectively to larger quantum processors. The implications of such a development extend beyond mere theoretical predictions; they embrace the potential for practical applications in advanced quantum technologies.
Looking ahead, the team aims to apply their innovative Hamiltonian learning techniques to other interacting quantum systems and explore the prospects of utilizing tensor networks in quantum experiments involving cold atoms. This inquiry revives a longstanding yet often underexplored question in quantum mechanics: how precisely can one define and learn the Hamiltonian of a system from experimental data? The necessity for accurate Hamiltonian characterization underlines the predictive power within quantum mechanics. Without precise knowledge of the Hamiltonian, theoretical predictions falter, drawing attention to the importance of robust Hamiltonian learning techniques.
Eisert anticipates that the advancements realized through this research will pave the way for significant developments in quantum technology. By enhancing the characterization of analog quantum simulators, these breakthroughs may open new avenues in the quest for high-precision quantum simulations. The potential to recreate complex quantum systems in laboratory settings under precise conditions is revolutionary; it not only enriches our understanding of quantum phenomena but also lays the groundwork for practical applications in quantum computing and material science.
The collaborative effort between interdisciplinary teams highlights the dynamic nature of quantum research. By addressing the pivotal question of Hamiltonian characterization, researchers are not just tackling academic inquiries; they are also contributing to the technological foundations that could redefine our interaction with quantum systems. As the field evolves, Eisert and his colleagues remain committed to advancing our comprehension of quantum mechanics, aiming to bridge the gap between theoretical understanding and experimental realization.

Leave a Reply